S.H.M. as Projection of U.C.M. Along any Diameter
S.H.M. as Projection of U.C.M. Along any Diameter: Overview
This topic covers concepts, such as, Circular Motion and SHM etc.
Important Questions on S.H.M. as Projection of U.C.M. Along any Diameter
For particle revolving round the centre with radius of circular path and regular velocity , as shown in below figure, the projection of on the -axis at time is
Define simple harmonic motion. Show that the motion of point projection of a particle performing circular motion, on any diameter, is circular motion.
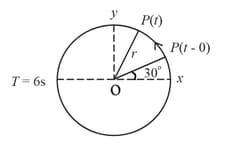
The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figure. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in this case.
The figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the figure. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in this case.
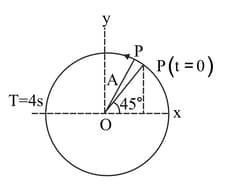
Suppose a particle P is moving uniformly on a circle of radius A with the angular speed . The sense of rotation is anticlockwise. If the , it makes an angle of with the positive direction of the x-axis. In time , it will cover a further angle .What is the projection of position vector on the X-axis at time .
If we tie a stone to the end of a string and move it with a constant angular speed in a horizontal plane about fixed point, the stone would perform a :
If the particle is moving in circular motion under SHM, then its x-projection is depending upon
The x-projection for a certain particle in circular motion under SHM with period of , amplitude of oscillation is and initial phase of is
The x-projection of the particle in circular motion under SHM is independent of initial phase of the particle.
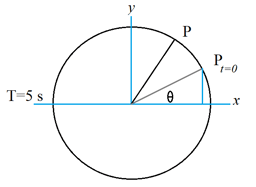
If a particle is in circular motion is under SHM moving to and fro about x-axis with period of and its initial angle made with horizontal axis is then find the projection of the particle after time if the amplitude of the particle under SHM is .
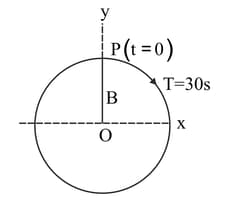
In the figure given below the period of revolution, the initial position and the sense of revolution are indicated. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P if the given figure depicts circular motion. (Here, )
The vibrations that are sustained under the action of an external periodic force are called Free oscillation
For a particle executing SHM, the phase difference between it's acceleration and displacement is _____ degrees.
Which of the following conditions is not sufficient for S.H.M. and why?
When a body is suspended by a spring is stretched. If the pulled down slightly and released, it oscillates up and down. What force is applied on the body by the spring when it passes through the mean position. .
Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to and , respectively. At time one particle has displacement while the other one has displacement and they are moving towards each other. If they cross each other at time , then is:
Time period and amplitude of a particle performing SHM along -axis is and respectively. The time taken by the particle to travel a distance after the particle started from rest is . The value of is:
In the given figure it corresponds to a circular motion. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on figure?

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P.
Plot the corresponding reference circle for simple harmonic motion. Indicate the initial position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in and t is in ).
In the given figure it corresponds to circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on the figure?

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P.
